Module: `transform`¶

`AffineTransform`¶

class skimage.transform.AffineTransform(matrix=None, scale=None, rotation=None, shear=None, translation=None)¶

Bases: skimage.transform._geometric.ProjectiveTransform

2D affine transformation of the form:

X = a0*x + a1*y + a2 =
  = sx*x*cos(rotation) - sy*y*sin(rotation + shear) + a2

Y = b0*x + b1*y + b2 =
  = sx*x*sin(rotation) + sy*y*cos(rotation + shear) + b2

where sx and sy are zoom factors in the x and y directions, and the homogeneous transformation matrix is:

[[a0  a1  a2]
 [b0  b1  b2]
 [0   0    1]]

Parameters:

Parameters:	matrix : (3, 3) array, optional Homogeneous transformation matrix. scale : (sx, sy) as array, list or tuple, optional Scale factors. rotation : float, optional Rotation angle in counter-clockwise direction as radians. shear : float, optional Shear angle in counter-clockwise direction as radians. translation : (tx, ty) as array, list or tuple, optional Translation parameters.

matrix : (3, 3) array, optional

Homogeneous transformation matrix.

scale : (sx, sy) as array, list or tuple, optional

Scale factors.

rotation : float, optional

Rotation angle in counter-clockwise direction as radians.

shear : float, optional

Shear angle in counter-clockwise direction as radians.

translation : (tx, ty) as array, list or tuple, optional

Translation parameters.

Attributes

params

(3, 3) array

Homogeneous transformation matrix.

__init__(matrix=None, scale=None, rotation=None, shear=None, translation=None)¶

rotation¶

scale¶

shear¶

translation¶

`PiecewiseAffineTransform`¶

class skimage.transform.PiecewiseAffineTransform¶

Bases: skimage.transform._geometric.GeometricTransform

2D piecewise affine transformation.

Control points are used to define the mapping. The transform is based on a Delaunay triangulation of the points to form a mesh. Each triangle is used to find a local affine transform.

Attributes

affines	list of AffineTransform objects	Affine transformations for each triangle in the mesh.
inverse_affines	list of AffineTransform objects	Inverse affine transformations for each triangle in the mesh.

__init__()¶

estimate(src, dst)¶

Set the control points with which to perform the piecewise mapping.

Number of source and destination coordinates must match.

Parameters:

Parameters:	src : (N, 2) array Source coordinates. dst : (N, 2) array Destination coordinates.

src : (N, 2) array

Source coordinates.

dst : (N, 2) array

Destination coordinates.

inverse(coords)¶

Apply inverse transformation.

Coordinates outside of the mesh will be set to - 1.

Parameters:

Parameters:	coords : (N, 2) array Source coordinates.
Returns:	coords : (N, 2) array Transformed coordinates.

coords : (N, 2) array

Source coordinates.

Returns:

coords : (N, 2) array

Transformed coordinates.

`PolynomialTransform`¶

class skimage.transform.PolynomialTransform(params=None)¶

Bases: skimage.transform._geometric.GeometricTransform

2D transformation of the form:

X = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i ))
Y = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i ))

Parameters:

Parameters:	params : (2, N) array, optional Polynomial coefficients where N * 2 = (order + 1) * (order + 2). So, a_ji is defined in params[0, :] and b_ji in params[1, :].

params : (2, N) array, optional

Polynomial coefficients where N * 2 = (order + 1) * (order + 2). So, a_ji is defined in params[0, :] and b_ji in params[1, :].

Attributes

__init__(params=None)¶

estimate(src, dst, order=2)¶

Set the transformation matrix with the explicit transformation parameters.

You can determine the over-, well- and under-determined parameters with the total least-squares method.

Number of source and destination coordinates must match.

The transformation is defined as:

X = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i ))
Y = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i ))

These equations can be transformed to the following form:

0 = sum[j=0:order]( sum[i=0:j]( a_ji * x**(j - i) * y**i )) - X
0 = sum[j=0:order]( sum[i=0:j]( b_ji * x**(j - i) * y**i )) - Y

which exist for each set of corresponding points, so we have a set of N * 2 equations. The coefficients appear linearly so we can write A x = 0, where:

A   = [[1 x y x**2 x*y y**2 ... 0 ...             0 -X]
       [0 ...                 0 1 x y x**2 x*y y**2 -Y]
        ...
        ...
      ]
x.T = [a00 a10 a11 a20 a21 a22 ... ann
       b00 b10 b11 b20 b21 b22 ... bnn c3]

In case of total least-squares the solution of this homogeneous system of equations is the right singular vector of A which corresponds to the smallest singular value normed by the coefficient c3.

Parameters:

Parameters:	src : (N, 2) array Source coordinates. dst : (N, 2) array Destination coordinates. order : int, optional Polynomial order (number of coefficients is order + 1).

src : (N, 2) array

Source coordinates.

dst : (N, 2) array

Destination coordinates.

order : int, optional

Polynomial order (number of coefficients is order + 1).

inverse(coords)¶

`ProjectiveTransform`¶

class skimage.transform.ProjectiveTransform(matrix=None)¶

Bases: skimage.transform._geometric.GeometricTransform

Matrix transformation.

Apply a projective transformation (homography) on coordinates.

For each homogeneous coordinate \mathbf{x} = [x, y, 1]^T, its target position is calculated by multiplying with the given matrix, H, to give H \mathbf{x}:

[[a0 a1 a2]
 [b0 b1 b2]
 [c0 c1 1 ]].

E.g., to rotate by theta degrees clockwise, the matrix should be:

[[cos(theta) -sin(theta) 0]
 [sin(theta)  cos(theta) 0]
 [0            0         1]]

or, to translate x by 10 and y by 20:

[[1 0 10]
 [0 1 20]
 [0 0 1 ]].

Parameters:

Parameters:	matrix : (3, 3) array, optional Homogeneous transformation matrix.

matrix : (3, 3) array, optional

Homogeneous transformation matrix.

Attributes

params

(3, 3) array

Homogeneous transformation matrix.

__init__(matrix=None)¶

estimate(src, dst)¶

Set the transformation matrix with the explicit transformation parameters.

You can determine the over-, well- and under-determined parameters with the total least-squares method.

Number of source and destination coordinates must match.

The transformation is defined as:

X = (a0*x + a1*y + a2) / (c0*x + c1*y + 1)
Y = (b0*x + b1*y + b2) / (c0*x + c1*y + 1)

These equations can be transformed to the following form:

0 = a0*x + a1*y + a2 - c0*x*X - c1*y*X - X
0 = b0*x + b1*y + b2 - c0*x*Y - c1*y*Y - Y

which exist for each set of corresponding points, so we have a set of N * 2 equations. The coefficients appear linearly so we can write A x = 0, where:

A   = [[x y 1 0 0 0 -x*X -y*X -X]
       [0 0 0 x y 1 -x*Y -y*Y -Y]
        ...
        ...
      ]
x.T = [a0 a1 a2 b0 b1 b2 c0 c1 c3]

In case of total least-squares the solution of this homogeneous system of equations is the right singular vector of A which corresponds to the smallest singular value normed by the coefficient c3.

In case of the affine transformation the coefficients c0 and c1 are 0. Thus the system of equations is:

A   = [[x y 1 0 0 0 -X]
       [0 0 0 x y 1 -Y]
        ...
        ...
      ]
x.T = [a0 a1 a2 b0 b1 b2 c3]

Parameters:

Parameters:	src : (N, 2) array Source coordinates. dst : (N, 2) array Destination coordinates.

src : (N, 2) array

Source coordinates.

dst : (N, 2) array

Destination coordinates.

inverse(coords)¶

Apply inverse transformation.

Parameters:

Parameters:	coords : (N, 2) array Source coordinates.
Returns:	coords : (N, 2) array Transformed coordinates.

coords : (N, 2) array

Source coordinates.

Returns:

coords : (N, 2) array

Transformed coordinates.

`SimilarityTransform`¶

class skimage.transform.SimilarityTransform(matrix=None, scale=None, rotation=None, translation=None)¶

Bases: skimage.transform._geometric.ProjectiveTransform

2D similarity transformation of the form:

X = a0 * x - b0 * y + a1 =
  = m * x * cos(rotation) - m * y * sin(rotation) + a1

Y = b0 * x + a0 * y + b1 =
  = m * x * sin(rotation) + m * y * cos(rotation) + b1

where m is a zoom factor and the homogeneous transformation matrix is:

[[a0  b0  a1]
 [b0  a0  b1]
 [0   0    1]]

Parameters:

Parameters:	matrix : (3, 3) array, optional Homogeneous transformation matrix. scale : float, optional Scale factor. rotation : float, optional Rotation angle in counter-clockwise direction as radians. translation : (tx, ty) as array, list or tuple, optional x, y translation parameters.

matrix : (3, 3) array, optional

Homogeneous transformation matrix.

scale : float, optional

Scale factor.

rotation : float, optional

Rotation angle in counter-clockwise direction as radians.

translation : (tx, ty) as array, list or tuple, optional

x, y translation parameters.

Attributes

params

(3, 3) array

Homogeneous transformation matrix.

__init__(matrix=None, scale=None, rotation=None, translation=None)¶

estimate(src, dst)¶

Set the transformation matrix with the explicit parameters.

You can determine the over-, well- and under-determined parameters with the total least-squares method.

Number of source and destination coordinates must match.

The transformation is defined as:

X = a0 * x - b0 * y + a1
Y = b0 * x + a0 * y + b1

These equations can be transformed to the following form:

0 = a0 * x - b0 * y + a1 - X
0 = b0 * x + a0 * y + b1 - Y

which exist for each set of corresponding points, so we have a set of N * 2 equations. The coefficients appear linearly so we can write A x = 0, where:

A   = [[x 1 -y 0 -X]
       [y 0  x 1 -Y]
        ...
        ...
      ]
x.T = [a0 a1 b0 b1 c3]

In case of total least-squares the solution of this homogeneous system of equations is the right singular vector of A which corresponds to the smallest singular value normed by the coefficient c3.

Parameters:

Parameters:	src : (N, 2) array Source coordinates. dst : (N, 2) array Destination coordinates.

src : (N, 2) array

Source coordinates.

dst : (N, 2) array

Destination coordinates.

rotation¶

scale¶

translation¶

`skimage.transform.downscale_local_mean`(...)	Down-sample N-dimensional image by local averaging.
`skimage.transform.estimate_transform`(ttype, ...)	Estimate 2D geometric transformation parameters.
`skimage.transform.frt2`(a)	Compute the 2-dimensional finite radon transform (FRT) for an n x n integer array.
`skimage.transform.hough_circle`(image, radius)	Perform a circular Hough transform.
`skimage.transform.hough_ellipse`	Perform an elliptical Hough transform.
`skimage.transform.hough_line`	Perform a straight line Hough transform.
`skimage.transform.hough_line_peaks`(hspace, ...)	Return peaks in hough transform.
`skimage.transform.ifrt2`(a)	Compute the 2-dimensional inverse finite radon transform (iFRT) for an (n+1) x n integer array.
`skimage.transform.integral_image`(x)	Integral image / summed area table.
`skimage.transform.integrate`(ii, r0, c0, r1, c1)	Use an integral image to integrate over a given window.
`skimage.transform.iradon`(radon_image[, ...])	Inverse radon transform.
`skimage.transform.iradon_sart`(radon_image[, ...])	Inverse radon transform
`skimage.transform.matrix_transform`(coords, ...)	Apply 2D matrix transform.
`skimage.transform.probabilistic_hough_line`	Return lines from a progressive probabilistic line Hough transform.
`skimage.transform.pyramid_expand`(image[, ...])	Upsample and then smooth image.
`skimage.transform.pyramid_gaussian`(image[, ...])	Yield images of the Gaussian pyramid formed by the input image.
`skimage.transform.pyramid_laplacian`(image[, ...])	Yield images of the laplacian pyramid formed by the input image.
`skimage.transform.pyramid_reduce`(image[, ...])	Smooth and then downsample image.
`skimage.transform.radon`(image[, theta, circle])	Calculates the radon transform of an image given specified projection angles.
`skimage.transform.rescale`(image, scale[, ...])	Scale image by a certain factor.
`skimage.transform.resize`(image, output_shape)	Resize image to match a certain size.
`skimage.transform.rotate`(image, angle[, ...])	Rotate image by a certain angle around its center.
`skimage.transform.swirl`(image[, center, ...])	Perform a swirl transformation.
`skimage.transform.warp`(image[, inverse_map, ...])	Warp an image according to a given coordinate transformation.
`skimage.transform.warp_coords`(coord_map, shape)	Build the source coordinates for the output pixels of an image warp.

downscale_local_mean¶

skimage.transform.downscale_local_mean(image, factors, cval=0)¶

Down-sample N-dimensional image by local averaging.

The image is padded with cval if it is not perfectly divisible by the integer factors.

In contrast to the 2-D interpolation in skimage.transform.resize and skimage.transform.rescale this function may be applied to N-dimensional images and calculates the local mean of elements in each block of size factors in the input image.

Parameters:

Parameters:	image : ndarray N-dimensional input image. factors : array_like Array containing down-sampling integer factor along each axis. cval : float, optional Constant padding value if image is not perfectly divisible by the integer factors.
Returns:	image : ndarray Down-sampled image with same number of dimensions as input image.

image : ndarray

N-dimensional input image.

factors : array_like

Array containing down-sampling integer factor along each axis.

cval : float, optional

Constant padding value if image is not perfectly divisible by the integer factors.

Returns:

image : ndarray

Down-sampled image with same number of dimensions as input image.

Examples

>>> a = np.arange(15).reshape(3, 5)
>>> a
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])
>>> downscale_local_mean(a, (2, 3))
array([[ 3.5,  4. ],
       [ 5.5,  4.5]])

estimate_transform¶

skimage.transform.estimate_transform(ttype, src, dst, **kwargs)¶

Estimate 2D geometric transformation parameters.

You can determine the over-, well- and under-determined parameters with the total least-squares method.

Number of source and destination coordinates must match.

Parameters:

Parameters:	ttype : {‘similarity’, ‘affine’, ‘piecewise-affine’, ‘projective’, ‘polynomial’} Type of transform. kwargs : array or int Function parameters (src, dst, n, angle): NAME / TTYPE FUNCTION PARAMETERS 'similarity' `src, `dst` 'affine' `src, `dst` 'piecewise-affine' `src, `dst` 'projective' `src, `dst` 'polynomial' `src, `dst`, `order` (polynomial order, default order is 2) Also see examples below.
Returns:	tform : `GeometricTransform` Transform object containing the transformation parameters and providing access to forward and inverse transformation functions.

ttype : {‘similarity’, ‘affine’, ‘piecewise-affine’, ‘projective’, ‘polynomial’}

Type of transform.

kwargs : array or int

Function parameters (src, dst, n, angle):

NAME / TTYPE        FUNCTION PARAMETERS
'similarity'        `src, `dst`
'affine'            `src, `dst`
'piecewise-affine'  `src, `dst`
'projective'        `src, `dst`
'polynomial'        `src, `dst`, `order` (polynomial order,
                                          default order is 2)

Also see examples below.

Returns:

tform : GeometricTransform

Transform object containing the transformation parameters and providing access to forward and inverse transformation functions.

Examples

>>> import numpy as np
>>> from skimage import transform as tf

>>> # estimate transformation parameters
>>> src = np.array([0, 0, 10, 10]).reshape((2, 2))
>>> dst = np.array([12, 14, 1, -20]).reshape((2, 2))

>>> tform = tf.estimate_transform('similarity', src, dst)

>>> np.allclose(tform.inverse(tform(src)), src)
True

>>> # warp image using the estimated transformation
>>> from skimage import data
>>> image = data.camera()

>>> warp(image, inverse_map=tform.inverse) 

>>> # create transformation with explicit parameters
>>> tform2 = tf.SimilarityTransform(scale=1.1, rotation=1,
...     translation=(10, 20))

>>> # unite transformations, applied in order from left to right
>>> tform3 = tform + tform2
>>> np.allclose(tform3(src), tform2(tform(src)))
True

frt2¶

skimage.transform.frt2(a)¶

Compute the 2-dimensional finite radon transform (FRT) for an n x n integer array.

Parameters:

Parameters:	a : array_like A 2-D square n x n integer array.
Returns:	FRT : 2-D ndarray Finite Radon Transform array of (n+1) x n integer coefficients.

a : array_like

A 2-D square n x n integer array.

Returns:

FRT : 2-D ndarray

Finite Radon Transform array of (n+1) x n integer coefficients.

hough_circle¶

skimage.transform.hough_circle(image, radius, normalize=True, full_output=False)¶

Perform a circular Hough transform.

Parameters:

Parameters:	image : (M, N) ndarray Input image with nonzero values representing edges. radius : ndarray Radii at which to compute the Hough transform. normalize : boolean, optional (default True) Normalize the accumulator with the number of pixels used to draw the radius. full_output : boolean, optional (default False) Extend the output size by twice the largest radius in order to detect centers outside the input picture.
Returns:	H : 3D ndarray (radius index, (M + 2R, N + 2R) ndarray) Hough transform accumulator for each radius. R designates the larger radius if full_output is True. Otherwise, R = 0.

image : (M, N) ndarray

Input image with nonzero values representing edges.

radius : ndarray

Radii at which to compute the Hough transform.

normalize : boolean, optional (default True)

Normalize the accumulator with the number of pixels used to draw the radius.

full_output : boolean, optional (default False)

Extend the output size by twice the largest radius in order to detect centers outside the input picture.

Returns:

H : 3D ndarray (radius index, (M + 2R, N + 2R) ndarray)

Hough transform accumulator for each radius. R designates the larger radius if full_output is True. Otherwise, R = 0.

hough_ellipse¶

skimage.transform.hough_ellipse()¶

Perform an elliptical Hough transform.

Parameters:

Parameters:	img : (M, N) ndarray Input image with nonzero values representing edges. threshold: int, optional (default 4) : Accumulator threshold value. accuracy : double, optional (default 1) Bin size on the minor axis used in the accumulator. min_size : int, optional (default 4) Minimal major axis length. max_size : int, optional Maximal minor axis length. (default None) If None, the value is set to the half of the smaller image dimension.
Returns:	result : ndarray with fields [(accumulator, y0, x0, a, b, orientation)] Where `(yc, xc)` is the center, `(a, b)` the major and minor axes, respectively. The orientation value follows skimage.draw.ellipse_perimeter convention.

img : (M, N) ndarray

Input image with nonzero values representing edges.

threshold: int, optional (default 4) :

Accumulator threshold value.

accuracy : double, optional (default 1)

Bin size on the minor axis used in the accumulator.

min_size : int, optional (default 4)

Minimal major axis length.

max_size : int, optional

Maximal minor axis length. (default None) If None, the value is set to the half of the smaller image dimension.

Returns:

result : ndarray with fields [(accumulator, y0, x0, a, b, orientation)]

Where (yc, xc) is the center, (a, b) the major and minor axes, respectively. The orientation value follows skimage.draw.ellipse_perimeter convention.

Notes

The accuracy must be chosen to produce a peak in the accumulator distribution. In other words, a flat accumulator distribution with low values may be caused by a too low bin size.

References

[R313]

Xie, Yonghong, and Qiang Ji. “A new efficient ellipse detection method.” Pattern Recognition, 2002. Proceedings. 16th International Conference on. Vol. 2. IEEE, 2002

Examples

>>> img = np.zeros((25, 25), dtype=np.uint8)
>>> rr, cc = ellipse_perimeter(10, 10, 6, 8)
>>> img[cc, rr] = 1
>>> result = hough_ellipse(img, threshold=8)
[(10, 10.0, 8.0, 6.0, 0.0, 10.0)]

hough_line¶

skimage.transform.hough_line()¶

Perform a straight line Hough transform.

Parameters:

Parameters:	img : (M, N) ndarray Input image with nonzero values representing edges. theta : 1D ndarray of double Angles at which to compute the transform, in radians. Defaults to -pi/2 .. pi/2
Returns:	H : 2-D ndarray of uint64 Hough transform accumulator. theta : ndarray Angles at which the transform was computed, in radians. distances : ndarray Distance values.

img : (M, N) ndarray

Input image with nonzero values representing edges.

theta : 1D ndarray of double

Angles at which to compute the transform, in radians. Defaults to -pi/2 .. pi/2

Returns:

H : 2-D ndarray of uint64

Hough transform accumulator.

theta : ndarray

Angles at which the transform was computed, in radians.

distances : ndarray

Distance values.

Notes

The origin is the top left corner of the original image. X and Y axis are horizontal and vertical edges respectively. The distance is the minimal algebraic distance from the origin to the detected line.

Examples

Generate a test image:

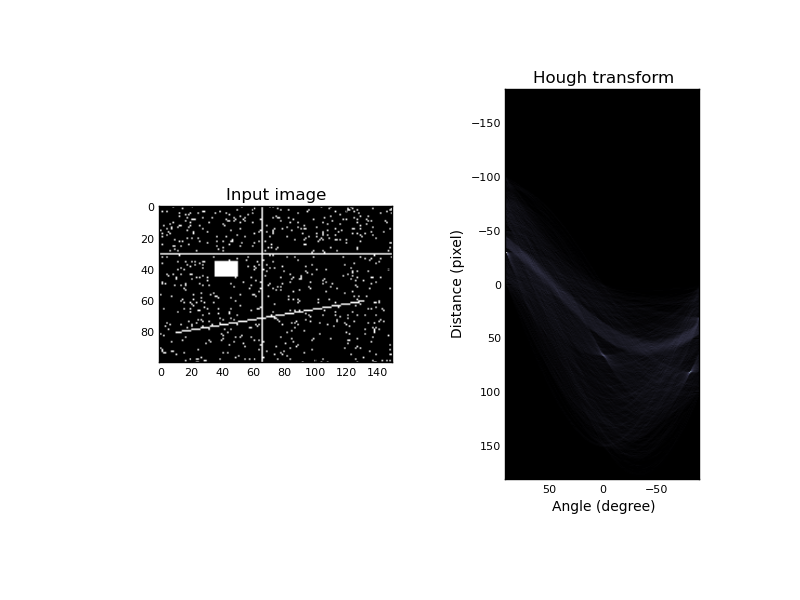
>>> img = np.zeros((100, 150), dtype=bool)
>>> img[30, :] = 1
>>> img[:, 65] = 1
>>> img[35:45, 35:50] = 1
>>> for i in range(90):
...     img[i, i] = 1
>>> img += np.random.random(img.shape) > 0.95

Apply the Hough transform:

>>> out, angles, d = hough_line(img)

import numpy as np
import matplotlib.pyplot as plt

from skimage.transform import hough_line
from skimage.draw import line

img = np.zeros((100, 150), dtype=bool)
img[30, :] = 1
img[:, 65] = 1
img[35:45, 35:50] = 1
rr, cc = line(60, 130, 80, 10)
img[rr, cc] = 1
img += np.random.random(img.shape) > 0.95

out, angles, d = hough_line(img)

plt.subplot(1, 2, 1)

plt.imshow(img, cmap=plt.cm.gray)
plt.title('Input image')

plt.subplot(1, 2, 2)
plt.imshow(out, cmap=plt.cm.bone,
           extent=(np.rad2deg(angles[-1]), np.rad2deg(angles[0]),
                   d[-1], d[0]))
plt.title('Hough transform')
plt.xlabel('Angle (degree)')
plt.ylabel('Distance (pixel)')

plt.subplots_adjust(wspace=0.4)
plt.show()

(Source code, png, pdf)

hough_line_peaks¶

skimage.transform.hough_line_peaks(hspace, angles, dists, min_distance=9, min_angle=10, threshold=None, num_peaks=inf)¶

Return peaks in hough transform.

Identifies most prominent lines separated by a certain angle and distance in a hough transform. Non-maximum suppression with different sizes is applied separately in the first (distances) and second (angles) dimension of the hough space to identify peaks.

Parameters:

Parameters:	hspace : (N, M) array Hough space returned by the hough_line function. angles : (M,) array Angles returned by the hough_line function. Assumed to be continuous. (angles[-1] - angles[0] == PI). dists : (N, ) array Distances returned by the hough_line function. min_distance : int Minimum distance separating lines (maximum filter size for first dimension of hough space). min_angle : int Minimum angle separating lines (maximum filter size for second dimension of hough space). threshold : float Minimum intensity of peaks. Default is 0.5 * max(hspace). num_peaks : int Maximum number of peaks. When the number of peaks exceeds num_peaks, return num_peaks coordinates based on peak intensity.
Returns:	hspace, angles, dists : tuple of array Peak values in hough space, angles and distances.

hspace : (N, M) array

Hough space returned by the hough_line function.

angles : (M,) array

Angles returned by the hough_line function. Assumed to be continuous. (angles[-1] - angles[0] == PI).

dists : (N, ) array

Distances returned by the hough_line function.

min_distance : int

Minimum distance separating lines (maximum filter size for first dimension of hough space).

min_angle : int

Minimum angle separating lines (maximum filter size for second dimension of hough space).

threshold : float

Minimum intensity of peaks. Default is 0.5 * max(hspace).

num_peaks : int

Maximum number of peaks. When the number of peaks exceeds num_peaks, return num_peaks coordinates based on peak intensity.

Returns:

hspace, angles, dists : tuple of array

Peak values in hough space, angles and distances.

Examples

>>> from skimage.transform import hough_line, hough_line_peaks
>>> from skimage.draw import line
>>> img = np.zeros((15, 15), dtype=np.bool_)
>>> rr, cc = line(0, 0, 14, 14)
>>> img[rr, cc] = 1
>>> rr, cc = line(0, 14, 14, 0)
>>> img[cc, rr] = 1
>>> hspace, angles, dists = hough_line(img)
>>> hspace, angles, dists = hough_line_peaks(hspace, angles, dists)
>>> len(angles)
2

ifrt2¶

skimage.transform.ifrt2(a)¶

Compute the 2-dimensional inverse finite radon transform (iFRT) for an (n+1) x n integer array.

Parameters:

Parameters:	a : array_like A 2-D (n+1) row x n column integer array.
Returns:	iFRT : 2-D n x n ndarray Inverse Finite Radon Transform array of n x n integer coefficients.

a : array_like

A 2-D (n+1) row x n column integer array.

Returns:

iFRT : 2-D n x n ndarray

Inverse Finite Radon Transform array of n x n integer coefficients.

integral_image¶

skimage.transform.integral_image(x)¶

Integral image / summed area table.

The integral image contains the sum of all elements above and to the left of it, i.e.:

S[m, n] = \sum_{i \leq m} \sum_{j \leq n} X[i, j]

Parameters:

Parameters:	x : ndarray Input image.
Returns:	S : ndarray Integral image / summed area table.

x : ndarray

Input image.

Returns:

S : ndarray

Integral image / summed area table.

References

[R315]

F.C. Crow, “Summed-area tables for texture mapping,” ACM SIGGRAPH Computer Graphics, vol. 18, 1984, pp. 207-212.

integrate¶

skimage.transform.integrate(ii, r0, c0, r1, c1)¶

Use an integral image to integrate over a given window.

Parameters:

Parameters:	ii : ndarray Integral image. r0, c0 : int or ndarray Top-left corner(s) of block to be summed. r1, c1 : int or ndarray Bottom-right corner(s) of block to be summed.
Returns:	S : scalar or ndarray Integral (sum) over the given window(s).

ii : ndarray

Integral image.

r0, c0 : int or ndarray

Top-left corner(s) of block to be summed.

r1, c1 : int or ndarray

Bottom-right corner(s) of block to be summed.

Returns:

S : scalar or ndarray

Integral (sum) over the given window(s).

iradon¶

skimage.transform.iradon(radon_image, theta=None, output_size=None, filter='ramp', interpolation='linear', circle=False)¶

Inverse radon transform.

Reconstruct an image from the radon transform, using the filtered back projection algorithm.

Parameters:

Parameters:	radon_image : array_like, dtype=float Image containing radon transform (sinogram). Each column of the image corresponds to a projection along a different angle. The tomography rotation axis should lie at the pixel index `radon_image.shape[0] // 2` along the 0th dimension of `radon_image`. theta : array_like, dtype=float, optional Reconstruction angles (in degrees). Default: m angles evenly spaced between 0 and 180 (if the shape of radon_image is (N, M)). output_size : int Number of rows and columns in the reconstruction. filter : str, optional (default ramp) Filter used in frequency domain filtering. Ramp filter used by default. Filters available: ramp, shepp-logan, cosine, hamming, hann. Assign None to use no filter. interpolation : str, optional (default ‘linear’) Interpolation method used in reconstruction. Methods available: ‘linear’, ‘nearest’, and ‘cubic’ (‘cubic’ is slow). circle : boolean, optional Assume the reconstructed image is zero outside the inscribed circle. Also changes the default output_size to match the behaviour of `radon` called with `circle=True`.
Returns:	reconstructed : ndarray Reconstructed image. The rotation axis will be located in the pixel with indices `(reconstructed.shape[0] // 2, reconstructed.shape[1] // 2)`.

radon_image : array_like, dtype=float

Image containing radon transform (sinogram). Each column of the image corresponds to a projection along a different angle. The tomography rotation axis should lie at the pixel index radon_image.shape[0] // 2 along the 0th dimension of radon_image.

theta : array_like, dtype=float, optional

Reconstruction angles (in degrees). Default: m angles evenly spaced between 0 and 180 (if the shape of radon_image is (N, M)).

output_size : int

Number of rows and columns in the reconstruction.

filter : str, optional (default ramp)

Filter used in frequency domain filtering. Ramp filter used by default. Filters available: ramp, shepp-logan, cosine, hamming, hann. Assign None to use no filter.

interpolation : str, optional (default ‘linear’)

Interpolation method used in reconstruction. Methods available: ‘linear’, ‘nearest’, and ‘cubic’ (‘cubic’ is slow).

circle : boolean, optional

Assume the reconstructed image is zero outside the inscribed circle. Also changes the default output_size to match the behaviour of radon called with circle=True.

Returns:

reconstructed : ndarray

Reconstructed image. The rotation axis will be located in the pixel with indices (reconstructed.shape[0] // 2, reconstructed.shape[1] // 2).

Notes

It applies the Fourier slice theorem to reconstruct an image by multiplying the frequency domain of the filter with the FFT of the projection data. This algorithm is called filtered back projection.

iradon_sart¶

skimage.transform.iradon_sart(radon_image, theta=None, image=None, projection_shifts=None, clip=None, relaxation=0.15)¶

Inverse radon transform

Reconstruct an image from the radon transform, using a single iteration of the Simultaneous Algebraic Reconstruction Technique (SART) algorithm.

Parameters:

Parameters:	radon_image : 2D array, dtype=float Image containing radon transform (sinogram). Each column of the image corresponds to a projection along a different angle. The tomography rotation axis should lie at the pixel index `radon_image.shape[0] // 2` along the 0th dimension of `radon_image`. theta : 1D array, dtype=float, optional Reconstruction angles (in degrees). Default: m angles evenly spaced between 0 and 180 (if the shape of radon_image is (N, M)). image : 2D array, dtype=float, optional Image containing an initial reconstruction estimate. Shape of this array should be `(radon_image.shape[0], radon_image.shape[0])`. The default is an array of zeros. projection_shifts : 1D array, dtype=float Shift the projections contained in `radon_image` (the sinogram) by this many pixels before reconstructing the image. The i’th value defines the shift of the i’th column of `radon_image`. clip : length-2 sequence of floats Force all values in the reconstructed tomogram to lie in the range `[clip[0], clip[1]]` relaxation : float Relaxation parameter for the update step. A higher value can improve the convergence rate, but one runs the risk of instabilities. Values close to or higher than 1 are not recommended.
Returns:	reconstructed : ndarray Reconstructed image. The rotation axis will be located in the pixel with indices `(reconstructed.shape[0] // 2, reconstructed.shape[1] // 2)`.

radon_image : 2D array, dtype=float

Image containing radon transform (sinogram). Each column of the image corresponds to a projection along a different angle. The tomography rotation axis should lie at the pixel index radon_image.shape[0] // 2 along the 0th dimension of radon_image.

theta : 1D array, dtype=float, optional

Reconstruction angles (in degrees). Default: m angles evenly spaced between 0 and 180 (if the shape of radon_image is (N, M)).

image : 2D array, dtype=float, optional

Image containing an initial reconstruction estimate. Shape of this array should be (radon_image.shape[0], radon_image.shape[0]). The default is an array of zeros.

projection_shifts : 1D array, dtype=float

Shift the projections contained in radon_image (the sinogram) by this many pixels before reconstructing the image. The i’th value defines the shift of the i’th column of radon_image.

clip : length-2 sequence of floats

Force all values in the reconstructed tomogram to lie in the range [clip[0], clip[1]]

relaxation : float

Relaxation parameter for the update step. A higher value can improve the convergence rate, but one runs the risk of instabilities. Values close to or higher than 1 are not recommended.

Returns:

reconstructed : ndarray

Reconstructed image. The rotation axis will be located in the pixel with indices (reconstructed.shape[0] // 2, reconstructed.shape[1] // 2).

Notes

Algebraic Reconstruction Techniques are based on formulating the tomography reconstruction problem as a set of linear equations. Along each ray, the projected value is the sum of all the values of the cross section along the ray. A typical feature of SART (and a few other variants of algebraic techniques) is that it samples the cross section at equidistant points along the ray, using linear interpolation between the pixel values of the cross section. The resulting set of linear equations are then solved using a slightly modified Kaczmarz method.

When using SART, a single iteration is usually sufficient to obtain a good reconstruction. Further iterations will tend to enhance high-frequency information, but will also often increase the noise.

References

[R316]

AC Kak, M Slaney, “Principles of Computerized Tomographic Imaging”, IEEE Press 1988.

[R317]

AH Andersen, AC Kak, “Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm”, Ultrasonic Imaging 6 pp 81–94 (1984)

[R318]

S Kaczmarz, “Angenäherte auflösung von systemen linearer gleichungen”, Bulletin International de l’Academie Polonaise des Sciences et des Lettres 35 pp 355–357 (1937)

[R319]

Kohler, T. “A projection access scheme for iterative reconstruction based on the golden section.” Nuclear Science Symposium Conference Record, 2004 IEEE. Vol. 6. IEEE, 2004.

[R320]

Kaczmarz’ method, Wikipedia, http://en.wikipedia.org/wiki/Kaczmarz_method

matrix_transform¶

skimage.transform.matrix_transform(coords, matrix)¶

Apply 2D matrix transform.

Parameters:

Parameters:	coords : (N, 2) array x, y coordinates to transform matrix : (3, 3) array Homogeneous transformation matrix.
Returns:	coords : (N, 2) array Transformed coordinates.

coords : (N, 2) array

x, y coordinates to transform

matrix : (3, 3) array

Homogeneous transformation matrix.

Returns:

coords : (N, 2) array

Transformed coordinates.

probabilistic_hough_line¶

skimage.transform.probabilistic_hough_line()¶

Return lines from a progressive probabilistic line Hough transform.

Parameters:

Parameters:	img : (M, N) ndarray Input image with nonzero values representing edges. threshold : int, optional (default 10) Threshold line_length : int, optional (default 50) Minimum accepted length of detected lines. Increase the parameter to extract longer lines. line_gap : int, optional, (default 10) Maximum gap between pixels to still form a line. Increase the parameter to merge broken lines more aggresively. theta : 1D ndarray, dtype=double, optional, default (-pi/2 .. pi/2) Angles at which to compute the transform, in radians.
Returns:	lines : list List of lines identified, lines in format ((x0, y0), (x1, y0)), indicating line start and end.

img : (M, N) ndarray

Input image with nonzero values representing edges.

threshold : int, optional (default 10)

Threshold

line_length : int, optional (default 50)

Minimum accepted length of detected lines. Increase the parameter to extract longer lines.

line_gap : int, optional, (default 10)

Maximum gap between pixels to still form a line. Increase the parameter to merge broken lines more aggresively.

theta : 1D ndarray, dtype=double, optional, default (-pi/2 .. pi/2)

Angles at which to compute the transform, in radians.

Returns:

lines : list

List of lines identified, lines in format ((x0, y0), (x1, y0)), indicating line start and end.

References

[R321]

C. Galamhos, J. Matas and J. Kittler, “Progressive probabilistic Hough transform for line detection”, in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1999.

pyramid_expand¶

skimage.transform.pyramid_expand(image, upscale=2, sigma=None, order=1, mode='reflect', cval=0)¶

Upsample and then smooth image.

Parameters:

Parameters:	image : array Input image. upscale : float, optional Upscale factor. sigma : float, optional Sigma for Gaussian filter. Default is 2 * upscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution. order : int, optional Order of splines used in interpolation of upsampling. See skimage.transform.warp for detail. mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’. cval : float, optional Value to fill past edges of input if mode is ‘constant’.
Returns:	out : array Upsampled and smoothed float image.

image : array

Input image.

upscale : float, optional

Upscale factor.

sigma : float, optional

Sigma for Gaussian filter. Default is 2 * upscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution.

order : int, optional

Order of splines used in interpolation of upsampling. See skimage.transform.warp for detail.

mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional

The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’.

cval : float, optional

Value to fill past edges of input if mode is ‘constant’.

Returns:

out : array

Upsampled and smoothed float image.

References

[R322]

http://web.mit.edu/persci/people/adelson/pub_pdfs/pyramid83.pdf

pyramid_gaussian¶

skimage.transform.pyramid_gaussian(image, max_layer=-1, downscale=2, sigma=None, order=1, mode='reflect', cval=0)¶

Yield images of the Gaussian pyramid formed by the input image.

Recursively applies the pyramid_reduce function to the image, and yields the downscaled images.

Note that the first image of the pyramid will be the original, unscaled image. The total number of images is max_layer + 1. In case all layers are computed, the last image is either a one-pixel image or the image where the reduction does not change its shape.

Parameters:

Parameters:	image : array Input image. max_layer : int Number of layers for the pyramid. 0th layer is the original image. Default is -1 which builds all possible layers. downscale : float, optional Downscale factor. sigma : float, optional Sigma for Gaussian filter. Default is 2 * downscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution. order : int, optional Order of splines used in interpolation of downsampling. See skimage.transform.warp for detail. mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’. cval : float, optional Value to fill past edges of input if mode is ‘constant’.
Returns:	pyramid : generator Generator yielding pyramid layers as float images.

image : array

Input image.

max_layer : int

Number of layers for the pyramid. 0th layer is the original image. Default is -1 which builds all possible layers.

downscale : float, optional

Downscale factor.

sigma : float, optional

Sigma for Gaussian filter. Default is 2 * downscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution.

order : int, optional

Order of splines used in interpolation of downsampling. See skimage.transform.warp for detail.

mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional

The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’.

cval : float, optional

Value to fill past edges of input if mode is ‘constant’.

Returns:

pyramid : generator

Generator yielding pyramid layers as float images.

References

[R323]

http://web.mit.edu/persci/people/adelson/pub_pdfs/pyramid83.pdf

pyramid_laplacian¶

skimage.transform.pyramid_laplacian(image, max_layer=-1, downscale=2, sigma=None, order=1, mode='reflect', cval=0)¶

Yield images of the laplacian pyramid formed by the input image.

Each layer contains the difference between the downsampled and the downsampled, smoothed image:

layer = resize(prev_layer) - smooth(resize(prev_layer))

Note that the first image of the pyramid will be the difference between the original, unscaled image and its smoothed version. The total number of images is max_layer + 1. In case all layers are computed, the last image is either a one-pixel image or the image where the reduction does not change its shape.

Parameters:

Parameters:	image : array Input image. max_layer : int Number of layers for the pyramid. 0th layer is the original image. Default is -1 which builds all possible layers. downscale : float, optional Downscale factor. sigma : float, optional Sigma for Gaussian filter. Default is 2 * downscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution. order : int, optional Order of splines used in interpolation of downsampling. See skimage.transform.warp for detail. mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’. cval : float, optional Value to fill past edges of input if mode is ‘constant’.
Returns:	pyramid : generator Generator yielding pyramid layers as float images.

image : array

Input image.

max_layer : int

Number of layers for the pyramid. 0th layer is the original image. Default is -1 which builds all possible layers.

downscale : float, optional

Downscale factor.

sigma : float, optional

Sigma for Gaussian filter. Default is 2 * downscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution.

order : int, optional

Order of splines used in interpolation of downsampling. See skimage.transform.warp for detail.

mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional

The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’.

cval : float, optional

Value to fill past edges of input if mode is ‘constant’.

Returns:

pyramid : generator

Generator yielding pyramid layers as float images.

References

[R324]

http://web.mit.edu/persci/people/adelson/pub_pdfs/pyramid83.pdf

[R325]

http://sepwww.stanford.edu/~morgan/texturematch/paper_html/node3.html

pyramid_reduce¶

skimage.transform.pyramid_reduce(image, downscale=2, sigma=None, order=1, mode='reflect', cval=0)¶

Smooth and then downsample image.

Parameters:

Parameters:	image : array Input image. downscale : float, optional Downscale factor. sigma : float, optional Sigma for Gaussian filter. Default is 2 * downscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution. order : int, optional Order of splines used in interpolation of downsampling. See skimage.transform.warp for detail. mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’. cval : float, optional Value to fill past edges of input if mode is ‘constant’.
Returns:	out : array Smoothed and downsampled float image.

image : array

Input image.

downscale : float, optional

Downscale factor.

sigma : float, optional

Sigma for Gaussian filter. Default is 2 * downscale / 6.0 which corresponds to a filter mask twice the size of the scale factor that covers more than 99% of the Gaussian distribution.

order : int, optional

Order of splines used in interpolation of downsampling. See skimage.transform.warp for detail.

mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional

The mode parameter determines how the array borders are handled, where cval is the value when mode is equal to ‘constant’.

cval : float, optional

Value to fill past edges of input if mode is ‘constant’.

Returns:

out : array

Smoothed and downsampled float image.

References

[R326]

http://web.mit.edu/persci/people/adelson/pub_pdfs/pyramid83.pdf

radon¶

skimage.transform.radon(image, theta=None, circle=False)¶

Calculates the radon transform of an image given specified projection angles.

Parameters:

Parameters:	image : array_like, dtype=float Input image. The rotation axis will be located in the pixel with indices `(image.shape[0] // 2, image.shape[1] // 2)`. theta : array_like, dtype=float, optional (default np.arange(180)) Projection angles (in degrees). circle : boolean, optional Assume image is zero outside the inscribed circle, making the width of each projection (the first dimension of the sinogram) equal to `min(image.shape)`.
Returns:	radon_image : ndarray Radon transform (sinogram). The tomography rotation axis will lie at the pixel index `radon_image.shape[0] // 2` along the 0th dimension of `radon_image`.
Raises:	ValueError : If called with `circle=True` and `image != 0` outside the inscribed circle

image : array_like, dtype=float

Input image. The rotation axis will be located in the pixel with indices (image.shape[0] // 2, image.shape[1] // 2).

theta : array_like, dtype=float, optional (default np.arange(180))

Projection angles (in degrees).

circle : boolean, optional

Assume image is zero outside the inscribed circle, making the width of each projection (the first dimension of the sinogram) equal to min(image.shape).

Returns:

radon_image : ndarray

Radon transform (sinogram). The tomography rotation axis will lie at the pixel index radon_image.shape[0] // 2 along the 0th dimension of radon_image.

Raises:

ValueError :

If called with circle=True and image != 0 outside the inscribed circle

rescale¶

skimage.transform.rescale(image, scale, order=1, mode='constant', cval=0.0)¶

Scale image by a certain factor.

Performs interpolation to upscale or down-scale images. For down-sampling N-dimensional images with integer factors by applying the arithmetic sum or mean, see skimage.measure.local_sum and skimage.transform.downscale_local_mean, respectively.

Parameters:

Parameters:	image : ndarray Input image. scale : {float, tuple of floats} Scale factors. Separate scale factors can be defined as (row_scale, col_scale).
Returns:	scaled : ndarray Scaled version of the input.
Other Parameters:
	order : int, optional The order of the spline interpolation, default is 1. The order has to be in the range 0-5. See skimage.transform.warp for detail. mode : string, optional Points outside the boundaries of the input are filled according to the given mode (‘constant’, ‘nearest’, ‘reflect’ or ‘wrap’). cval : float, optional Used in conjunction with mode ‘constant’, the value outside the image boundaries.

image : ndarray

Input image.

scale : {float, tuple of floats}

Scale factors. Separate scale factors can be defined as (row_scale, col_scale).

Returns:

scaled : ndarray

Scaled version of the input.

Other Parameters:

order : int, optional

The order of the spline interpolation, default is 1. The order has to be in the range 0-5. See skimage.transform.warp for detail.

mode : string, optional

Points outside the boundaries of the input are filled according to the given mode (‘constant’, ‘nearest’, ‘reflect’ or ‘wrap’).

cval : float, optional

Used in conjunction with mode ‘constant’, the value outside the image boundaries.

Examples

>>> from skimage import data
>>> from skimage.transform import rescale
>>> image = data.camera()
>>> rescale(image, 0.1).shape
(51, 51)
>>> rescale(image, 0.5).shape
(256, 256)

resize¶

skimage.transform.resize(image, output_shape, order=1, mode='constant', cval=0.0)¶

Resize image to match a certain size.

Performs interpolation to up-size or down-size images. For down-sampling N-dimensional images by applying the arithmetic sum or mean, see skimage.measure.local_sum and skimage.transform.downscale_local_mean, respectively.

Parameters:

image : ndarray

Input image.

output_shape : tuple or ndarray

Size of the generated output image (rows, cols[, dim]). If dim is not provided, the number of channels is preserved. In case the number of input channels does not equal the number of output channels a 3-dimensional interpolation is applied.

Returns:

resized : ndarray

Resized version of the input.

Other Parameters:

order : int, optional

The order of the spline interpolation, default is 1. The order has to be in the range 0-5. See skimage.transform.warp for detail.

mode : string, optional

Points outside the boundaries of the input are filled according to the given mode (‘constant’, ‘nearest’, ‘reflect’ or ‘wrap’).

cval : float, optional

Used in conjunction with mode ‘constant’, the value outside the image boundaries.

Examples

>>> from skimage import data
>>> from skimage.transform import resize
>>> image = data.camera()
>>> resize(image, (100, 100)).shape
(100, 100)

rotate¶

skimage.transform.rotate(image, angle, resize=False, order=1, mode='constant', cval=0.0)¶

Rotate image by a certain angle around its center.

Parameters:

image : ndarray

Input image.

angle : float

Rotation angle in degrees in counter-clockwise direction.

resize : bool, optional

Determine whether the shape of the output image will be automatically calculated, so the complete rotated image exactly fits. Default is False.

Returns:

rotated : ndarray

Rotated version of the input.

Other Parameters:

order : int, optional

The order of the spline interpolation, default is 1. The order has to be in the range 0-5. See skimage.transform.warp for detail.

mode : string, optional

Points outside the boundaries of the input are filled according to the given mode (‘constant’, ‘nearest’, ‘reflect’ or ‘wrap’).

cval : float, optional

Used in conjunction with mode ‘constant’, the value outside the image boundaries.

Examples

>>> from skimage import data
>>> from skimage.transform import rotate
>>> image = data.camera()
>>> rotate(image, 2).shape
(512, 512)
>>> rotate(image, 2, resize=True).shape
(530, 530)
>>> rotate(image, 90, resize=True).shape
(512, 512)

swirl¶

skimage.transform.swirl(image, center=None, strength=1, radius=100, rotation=0, output_shape=None, order=1, mode='constant', cval=0)¶

Perform a swirl transformation.

Parameters:

image : ndarray

Input image.

center : (x,y) tuple or (2,) ndarray, optional

Center coordinate of transformation.

strength : float, optional

The amount of swirling applied.

radius : float, optional

The extent of the swirl in pixels. The effect dies out rapidly beyond radius.

rotation : float, optional

Additional rotation applied to the image.

Returns:

swirled : ndarray

Swirled version of the input.

Other Parameters:

output_shape : tuple (rows, cols), optional

Shape of the output image generated. By default the shape of the input image is preserved.

order : int, optional

The order of the spline interpolation, default is 1. The order has to be in the range 0-5. See skimage.transform.warp for detail.

mode : string, optional

Points outside the boundaries of the input are filled according to the given mode (‘constant’, ‘nearest’, ‘reflect’ or ‘wrap’).

cval : float, optional

Used in conjunction with mode ‘constant’, the value outside the image boundaries.

warp¶

skimage.transform.warp(image, inverse_map=None, map_args={}, output_shape=None, order=1, mode='constant', cval=0.0, reverse_map=None)¶

Warp an image according to a given coordinate transformation.

Parameters:

image : 2-D or 3-D array

Input image.

inverse_map : transformation object, callable xy = f(xy, **kwargs), (3, 3) array

Inverse coordinate map. A function that transforms a (N, 2) array of (x, y) coordinates in the output image into their corresponding coordinates in the source image (e.g. a transformation object or its inverse). See example section for usage.

map_args : dict, optional

Keyword arguments passed to inverse_map.

output_shape : tuple (rows, cols), optional

Shape of the output image generated. By default the shape of the input image is preserved.

order : int, optional

The order of interpolation. The order has to be in the range 0-5: * 0: Nearest-neighbor * 1: Bi-linear (default) * 2: Bi-quadratic * 3: Bi-cubic * 4: Bi-quartic * 5: Bi-quintic

mode : string, optional

Points outside the boundaries of the input are filled according to the given mode (‘constant’, ‘nearest’, ‘reflect’ or ‘wrap’).

cval : float, optional

Used in conjunction with mode ‘constant’, the value outside the image boundaries.

Notes

In case of a SimilarityTransform, AffineTransform and ProjectiveTransform and order in [0, 3] this function uses the underlying transformation matrix to warp the image with a much faster routine.

Examples

>>> from skimage.transform import warp
>>> from skimage import data
>>> image = data.camera()

The following image warps are all equal but differ substantially in execution time. The image is shifted to the bottom.

Use a geometric transform to warp an image (fast):

>>> from skimage.transform import SimilarityTransform
>>> tform = SimilarityTransform(translation=(0, -10))
>>> warped = warp(image, tform)

Use a callable (slow):

>>> def shift_down(xy):
...     xy[:, 1] -= 10
...     return xy
>>> warped = warp(image, shift_down)

Use a transformation matrix to warp an image (fast):

>>> matrix = np.array([[1, 0, 0], [0, 1, -10], [0, 0, 1]])
>>> warped = warp(image, matrix)
>>> from skimage.transform import ProjectiveTransform
>>> warped = warp(image, ProjectiveTransform(matrix=matrix))

You can also use the inverse of a geometric transformation (fast):

>>> warped = warp(image, tform.inverse)

warp_coords¶

skimage.transform.warp_coords(coord_map, shape, dtype=<type 'numpy.float64'>)¶

Build the source coordinates for the output pixels of an image warp.

Parameters:

coord_map : callable like GeometricTransform.inverse

Return input coordinates for given output coordinates. Coordinates are in the shape (P, 2), where P is the number of coordinates and each element is a (x, y) pair.

shape : tuple

Shape of output image (rows, cols[, bands]).

dtype : np.dtype or string

dtype for return value (sane choices: float32 or float64).

Returns:

coords : (ndim, rows, cols[, bands]) array of dtype dtype

Coordinates for scipy.ndimage.map_coordinates, that will yield an image of shape (orows, ocols, bands) by drawing from source points according to the coord_transform_fn.

Notes

This is a lower-level routine that produces the source coordinates used by warp().

It is provided separately from warp to give additional flexibility to users who would like, for example, to re-use a particular coordinate mapping, to use specific dtypes at various points along the the image-warping process, or to implement different post-processing logic than warp performs after the call to ndimage.map_coordinates.

Examples

Produce a coordinate map that Shifts an image up and to the right:

>>> from skimage import data
>>> from scipy.ndimage import map_coordinates
>>>
>>> def shift_up10_left20(xy):
...     return xy - np.array([-20, 10])[None, :]
>>>
>>> image = data.lena().astype(np.float32)
>>> coords = warp_coords(shift_up10_left20, image.shape)
>>> warped_image = map_coordinates(image, coords)

Module: `transform`¶

`AffineTransform`¶

`PiecewiseAffineTransform`¶

`PolynomialTransform`¶

`ProjectiveTransform`¶

`SimilarityTransform`¶

downscale_local_mean¶

estimate_transform¶

frt2¶

hough_circle¶

hough_ellipse¶

hough_line¶

hough_line_peaks¶

ifrt2¶

integral_image¶

integrate¶

iradon¶

iradon_sart¶

matrix_transform¶

probabilistic_hough_line¶

pyramid_expand¶

pyramid_gaussian¶

pyramid_laplacian¶

pyramid_reduce¶

radon¶

rescale¶

resize¶

rotate¶

swirl¶

warp¶

warp_coords¶

Navigation

Contents

Versions

Module: transform¶

AffineTransform¶

PiecewiseAffineTransform¶

PolynomialTransform¶

ProjectiveTransform¶

SimilarityTransform¶

downscale_local_mean¶

estimate_transform¶

frt2¶

hough_circle¶

hough_ellipse¶

hough_line¶

hough_line_peaks¶

ifrt2¶

integral_image¶

integrate¶

iradon¶

iradon_sart¶

matrix_transform¶

probabilistic_hough_line¶

pyramid_expand¶

pyramid_gaussian¶

pyramid_laplacian¶

pyramid_reduce¶

radon¶

rescale¶

resize¶

rotate¶

swirl¶

warp¶

warp_coords¶

Navigation

Contents

Versions

Module: `transform`¶

`AffineTransform`¶

`PiecewiseAffineTransform`¶

`PolynomialTransform`¶

`ProjectiveTransform`¶

`SimilarityTransform`¶